Coherent Potential Approximation (CPA)
There is currently no quantum mechanical transport model for charge (or phonon) transport in multiphase nanocrystalline structures. Due to absence of periodicity, one cannot apply any of the elegant theorems, such as Bloch’s theorem, which are implicit in the basic theory of crystalline solids. Atomistic models such as Kubo and NEGF may assume an accurate knowledge of the interatomic potentials; however, calculations for real 3D random multi-phase systems require so large computational times that makes them practically impossible. Many approximate approaches have been proposed to calculate the electronic properties of disordered alloys.
The Coherent Potential Approximation (CPA) has been shown to be one of the most effective out of a class of theories known as “single-cell” theories. It can successfully predict the major trends in the band structures of alloys as a function of their composition. Nevertheless, it remains relatively simple from computational point of view unlike the first principles calculations which treat only the system geometries with long range periodicity.
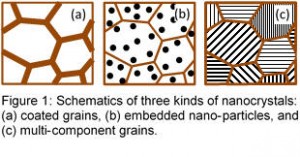
The physical processes in each individual grain no longer follow the well described classical continuum linear transport theory. Therefore, a proper model for coupled transport of charge carriers and phonons that takes into account the effect of their non-equilibrium energy distribution is highly desirable. In a multi-phase nanocrystalline material, grains and interfacial microstructures may have three distinct types as depicted in Figure 1.
Achievements
We developed two new theories and associated codes based on Coherent Potential Approximation (CPA) one for electron transport and one for phonon transport. The codes calculate the charge and phonon transport parameters in nanocomposite structures. These can be nano-crystalline (symmetric case) or the material with embedded nano-particles (asymmetric case). CPA specifically considers muli-scattering effect that cannot be explained with other semi-classical methods such as Partial Wave or Fermi’s golden rule. To our knowledge this is the first CPA code developed to study both electron and phonon transport in nanocomposite structures.
We also developed a multiband electron transport simulator based on BTE coupled with phonon transport based on Callaway model of thermal conductivity. We added the effect of magnetic field to our multiband electron transport simulator. The code is unique as the derived equations are valid for an arbitrary strength of the magnetic field (weak to strong). To our knowledge this is the first calculation with no approximation based on the strength of the magnetic field. The code will be extremely useful for designing/optimizing thermomagnetic materials. This project was funded by NSF the thermal transport processes program. The code can be extend to different types of nanocrystalline materials taking into account the average grain size, as well as the grain size distribution, and volume fraction of the different constituents in the materials. This is a strong tool that can describe more complex systems such as nanocrystals with randomly oriented grains with predictive power for the properties of electrical and thermal properties of disordered nanocomposites.
Integrated First principles-CPA-BTE solver
 Due to the complexity of the thermoelectric material systems, full first principles calculations are not practical; therefore, we have combined the three different frameworks based on first principle calculations, Coherent Potential Approximation (CPA), and multiband Boltzmann transport equation (BTE) to design and sturdy the thermoelectric materials. Figure 2 depicts the overall block diagram of the calculations.
Due to the complexity of the thermoelectric material systems, full first principles calculations are not practical; therefore, we have combined the three different frameworks based on first principle calculations, Coherent Potential Approximation (CPA), and multiband Boltzmann transport equation (BTE) to design and sturdy the thermoelectric materials. Figure 2 depicts the overall block diagram of the calculations.
Based on theoretical computations, we have recently predicted an extraordinarily large thermoelectric power factor for type-VIII clathrate Si46 due the existence of a large density of closely packed carier pockets near the band edges of this so far hypothetical material structure (Figure 3). Our first principles calculations have predicted a high crystallographic symmetry near both the band edges for Si46-VIII clathrate. We calculated the predicted thermoelectric transport properties both for the bulk crystalline and nanostructured Si46-VIII clathrates. The calculations were based on multiband Boltzamann transport equation and the data from density functional theory and molecular dynamics simulations. The predicted figure-of-merit of bulk nanostructured p-type Si46-VIII clathrate is in the order of 2 at 1000 C, which is higher than that of the best high temperature thermoelectric materials known today.
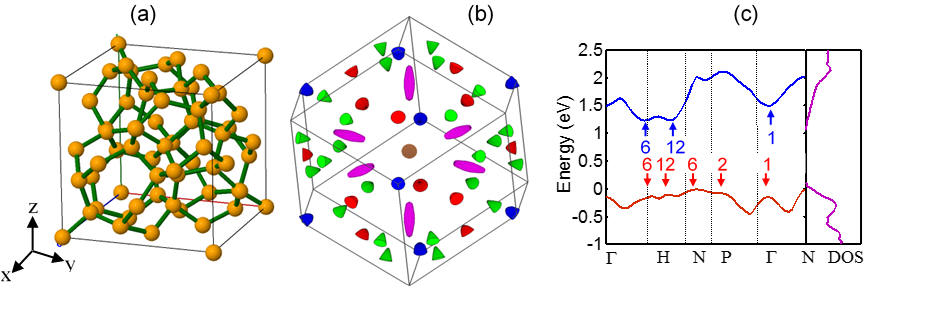
Figure 3: (a) Crystal structure of the type-VIII clathrate Si46 in real space. (b) Brillouin zone of the Si46 type VIII clathrate showing the hole pockets at Γ= (0, 0, 0) point (orange), on the ΓH line (violet), on the NH line (green), at P= (1/4, 1/4, 1/4) point (blue), and at N= (1/2, 0, 0) points (red). The valley degeneracies for Γ, N, P, ΓH and NH are 1, 6, 2, 6, and 12, respectively. (c) The predicted conduction and valance band structures and the densities of states.
Representative Publications
- Electronic, elastic, vibrational, and thermodynamic properties of type-VIII clathrates Ba8Ga16Sn30 and Ba8Al16Sn30 by first principles, P. Norouzzadeh, C. W. Myles, and D. Vashaee, J. Appl. Phys. 114, 163509 (2013).
- Prediction of a large number of electron pockets near the band edges in type-VIII clathrate Si46 and its physical properties from first principles, P. Norouzzadeh, C. W. Myles, and D. Vashaee, J. Phys.: Condens. Matter 25, 475502 (2013).
- Structural, electronic, phonon and thermodynamic properties of hypothetical type-VIII clathrates Ba8Si46 and Ba8Al16Si30 from first principles, P. Norouzzadeh, C. W. Myles, and D. Vashaee, Journal of Alloys and Compounds, http://www.sciencedirect.com/science/article/pii/ S0925838813026169 (2013).
- The effect of crystallite size on thermoelectric properties of bulk nanostructured Magnesium Silicide (Mg2Si) compounds, Nikhil Satyala, Daryoosh Vashaee, Appl. Phys. Lett. 100, 073107 (2012)
- The effect of nanostructuring on thermoelectric transport properties of p-type higher manganese silicide MnSi1.73, Payam Norouzzadeh, Zahra Zamanipour, Jerzy Krasinski, Daryoosh Vashaee, J. of Applied Physics, 112, 124308 (2012); doi: 10.1063/1.4769884
- Detrimental influence of nanostructuring on the thermoelectric properties of magnesium silicide, Nikhil Satyala and Daryoosh Vashaee, J. of Applied Physics, DOI: 10.1063/1.4764872 (2012)
- Modeling of Thermoelectric Properties of Magnesium Silicide (Mg2Si) , Nikhil Satyala, Daryoosh Vashaee, Journal of Electronic Materials, vol. 499, no. 1, pp. 68-1791 (2012)
- Modeling study of thermoelectric SiGe nanocomposites, A. J. Minnich, H. Lee, X. W. Wang, G. Joshi, M. S. Dresselhaus, Z. F. Ren, G. Chen, and D. Vashaee, , Physical Review B 80, 155327 (2009)
- Modeling Grain Boundary Scattering in Nanocomposites, Austin Minnich, Daryoosh Vashaee, Gang Chen, Proceedings of IMECE 2008 ASME International Engineering Conference and Exhibition October 31- November 6, 2008, Boston, Massachusetts.
- Thermoelectric transport in Silicon Germanium nanocomposite, Hohyun Lee, Daryoosh Vashaee, Xiaowei Wang, Giri Joshi, Gaohua Zhu, Dezhi Wang, Zhifeng Ren, Sabah Bux, Richard Blair, Pawan Gogna, Jean-Pierre Fleurial, Ming Y. Tang, Mildred S. Dresselhaus, Gang Chen, ASME International Mechanical Engineering Congress and Exposition IMECE October 31 – November 6, 2008, Boston, Massachusetts, USA
- The Effect of Grain Size and Volume Fraction on Charge Transport in Thermoelectric Nanocomposite of Bi2Te3-Sb2Te3, Payam Norouzzadeh, Daryoosh Vashaee, IEEE Green Technologies Conference 2012 – Energy Generation & Storage Technologies, Tulsa, Oklahoma, April 19-20, 2012